* 공부 정리일자 (2022년 8월 ~ 12월)
- 책 : 데이터베이스 배움터 (ORACLE을 기반으로 하는), 데이터베이스 개론 (2판), 데이터베이스 시스템 (해외서적 6판)
- 개인적으로 공부 및 복습하면서 정리한 내용입니다. (사진 제외)
* 목차
3.1) 관계 대수와 SQL
3.2) 관계 연산자들의 종류 (필수적인 연산자)
(1) 필수적인 연산자 – 실렉션 연산자, 선택 연산 (Selection Operation)
(2) 필수적인 연산자 – 프로젝션 연산자, 추출 연산 (Projection Operation)
(3) 필수적인 연산자 – 집합 연산자
(4) 필수적인 연산자 – 집합 연산자 – 합집합 연산 (Union Operation)
(5) 필수적인 연산자 – 집합 연산자 – 교집합 연산자 (intersection)
(6) 필수적인 연산자 – 집합 연산자 – 차집합 연산자 (Set Difference Operation)
(7) 필수적인 연산자 - 카티션 곱 연산자 (Cartesian-Product Operation)
(8) 관계 대수의 완전성
3.3) 관계 연산자들의 종류 (편의를 위해 유도된 연산자)
(1) 편의유도 연산자 – 복합 연산 (Composition of Operations)
(2) 재명명 연산 (rename operation)
(3) 형식적 정의 (Formal Definition)
(4) 편의유도 연산자 - 조인 연산자
(4.1, 4.2) 편의유도 연산자 – 조인 연산자 - 세타 조인 (theta join)과 동등 조인 (equijoin)
(4.3) 편의유도 연산자 – 조인 연산자 – 자연 조인 (natural join)
(5) 디비전 연산자, 나누기 계산 (Division Operation)
3.4) 추가된 관계 대수 연산자
(1) 외부 조인 (Outer Join)
(2) 그룹화
(3) 확장 관계형 대수 연산 – 일반화 추출
(4) 확장 관계형 대수 연산 – 집단 함수 (Aggregate Functions)
1. 복습 (중요 키워드 위주)
* 복습 파트 : 3강. 관계 대수 (관계 데이터 모델)
3.1) 관계 대수와 SQL
(1) 관계 데이터 모델에서 지원되는 두 가지 정형적인 언어
* 관계 해석 (relational calculus)
- 원하는 데이터만 명시하고 질의를 어떻게 수행할 것인가는 명시하지 않는 선언적인 언어
* 관계 대수 , 관계형 대수 (relational algebra)
- 어떻게 질의를 수행할 것인가를 명시하는 절차적 인어
- 관계 대수는 상용 관계 DBMS들에서 널리 사용되는 SQL의 이론적인 기초
- 관계 대수는 SQL을 구현하고 최적화하기 위해 DBMS의 내부 언어로서도 사용됨
- 연산자는 입력으로서 하나 이상의 릴레이션을 취해 그 결과로 새로운 릴레이션을 생성한다.
(2) SQL
- 상용 관계 DBMS들의 사실상의 표준 질의어
- 사용자는 SQL을 사용하여 1> 관계 데이터베이스에 릴레이션을 정의하고,
2> 관계 데이터베이스에서 정보를 검색하고, 3> 관계 데이터베이스를 갱신하며,
4> 여러 가지 무결성 제약조건들을 명시할 수 있음
(3) 관계 대수
- 기존의 릴레이션들로부터 새로운 릴레이션을 생성함.
- 릴레이션이나 관계 대수식(이것의 결과도 릴레이션임)에
연산자들을 적용하여 보다 복잡한 관계 대수식을 점차적으로 만들 수 있음
- 기본적인 연산자들의 집합으로 이루어짐
- 산술 연산자와 유사하게 단일 릴레이션이나 두 개의 릴레이션을 입력으로 받아 하나의 결과 릴레이션을 생성함
- 결과 릴레이션은 또 다른 관계 연산자의 입력으로 사용될 수 있음
- 연산대상(피연산자) : 릴레이션
- 연산자 : 기본 관계연산들
(4) 관계 대수의 한계
- 관계 대수는 산술 연산을 할 수 없음
- 집단 함수(aggregate function)를 지원하지 않음
- 정렬을 나타낼 수 없음
- 데이터베이스를 수정할 수 없음
- 프로젝션 연산의 결과에 중복된 투플을 나타내는 것이 필요할 때가 있는데 이를 명시하지 못함
* 6 가지 기본 연산자
- 선택 / 추출 / 합집합 / 차집합 / 카티전 곱 / 재명명

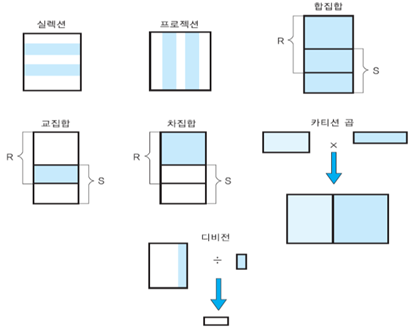
3.2) 관계 연산자들의 종류 (필수적인 연산자)
(1) 필수적인 연산자 – 실렉션 연산자, 선택 연산 (Selection Operation)
- 한 릴레이션에서 실렉션 조건(selection condition)을 만족하는 투플들의 부분 집합을 생성함
(2) 필수적인 연산자 – 프로젝션 연산자, 추출 연산 (Projection Operation)
- 한 릴레이션의 애트리뷰트들의 부분 집합을 구함
- 결과로 생성되는 릴레이션은 <애트리뷰트 리스트>에 명시된 애트리뷰트들만 가짐
- 실렉션의 결과
릴레이션에는 중복 투플이 존재할 수 없지만,
프로젝션 연산의 결과 릴레이션에는 중복된 투플들이 존재할 수 있음 (X)
(3) 필수적인 연산자 – 집합 연산자
- 릴레이션이 투플들의 집합이기 때문에 기존의 집합 연산이 릴레이션에 적용됨
- 세 가지 집합 연산자 : 합집합, 교집합, 차집합 연산자
- 집합 연산자의 입력으로 사용되는 두 개의 릴레이션은 합집합 호환(union compatible)이어야 함
(4) 필수적인 연산자 – 집합 연산자 – 합집합 연산 (Union Operation)
* 표기법 : r U s
* 다음과 같이 정의 한다 : r U s = {t | t ∈ r or t ∈ s}
- 두 릴레이션 R과 S의 합집합 R ∪ S는 R 또는 S에 있거나 R과 S 모두에 속한 투플들로 이루어진 릴레이션
- 결과 릴레이션에서 중복된 투플들은 제외됨
- 결과 릴레이션의 차수는
R 또는 S의 차수와 같으며,
결과 릴레이션의 애트리뷰트 이름들은 R의 애트리뷰트들의 이름과 같거나 S의 애트리뷰트들의 이름과 같음
(5) 필수적인 연산자 – 집합 연산자 – 교집합 연산자 (intersection)
* 표기법: r ∩ s
* 다음과 같이 정의된다 : r ∩ s = {t | t ∈ r and t ∈ s}
- 두 릴레이션 R과 S의 교집합 R ∩ S는 R과 S 모두에 속한 투플들로 이루어진 릴레이션
- 결과 릴레이션의 차수는
R 또는 S의 차수와 같으며,
결과 릴레이션의 애트리뷰트 이름들은 R의 애트리뷰트들의 이름과 같거나 S의 애트리뷰트들의 이름과 같음
(6) 필수적인 연산자 – 집합 연산자 – 차집합 연산자 (Set Difference Operation)
* 표기법 : r – s
* 다음과 같이 정의된다 : r – s = {t | t ∈ r and t ∉ s}
- 두 릴레이션 R과 S의 차집합 R - S는 R에는 속하지만 S에는 속하지 않은 투플들로 이루어진 릴레이션
- 결과 릴레이션의 차수는
R 또는 S의 차수와 같으며,
결과 릴레이션의 애트리뷰트 이름들은 R의 애트리뷰트들의 이름과 같거나 S의 애트리뷰트들의 이름과 같음
(7) 필수적인 연산자 - 카티션 곱 연산자 (Cartesian-Product Operation)
* 표기법 : r x s
* 다음과 같이 정의 된다 : r x s = {t q| t ∈ r and q ∈ s}
- 카디날리티가 i인 릴레이션 R(A1, A2, ..., An)과 카디날리티가 j인 릴레이션 S(B1, B2, ..., Bm)의
카티션 곱 R × S는 차수가 n+m이고,
카디날리티가 i*j이고,
애트리뷰트가 (A1, A2, ..., An, B1, B2, ..., Bm)이며,
R과 S의 투플들의 모든 가능한 조합으로 이루어진 릴레이션
(8) 관계 대수의 완전성
- 실렉션, 프로젝션, 합집합, 차집합, 카티션 곱은 관계 대수의 필수적인 연산자
- 다른 관계 연산자들은 필수적인 관계 연산자를 두 개 이상 조합하여 표현할 수 있음
- 임의의 질의어가 적어도
필수적인 관계 대수 연산자들만큼의 표현력을 갖고 있으면 관계적으로 완전(relationally complete)하다고 말함
3.3) 관계 연산자들의 종류 (편의를 위해 유도된 연산자)
(1) 편의유도 연산자 – 복합 연산 (Composition of Operations)
* 여러 연산을 사용해 표현식을 만들 수 있다.
* 예 : (r x s)
(2) 재명명 연산 (rename operation)
* 이름을 줄 수 있도록 하여 관계형 대수 표현식의 결과를 참조하도록 한다.
(3) 형식적 정의 (Formal Definition)
* 관계형 대수에서의 기본 표현식은 다음 중 하나 이상으로 구성된다.
- 데이터베이스내의 릴레이션
- 상수 릴레이션
(4) 편의유도 연산자 - 조인 연산자
- 두 개의 릴레이션으로부터 연관된 투플들을 결합하는 연산자
- 관계 데이터베이스에서 두 개 이상의 릴레이션들의 관계를 다루는데 매우 중요한 연산자
- 세타 조인(theta join), 동등 조인(equijoin), 자연 조인(natural join), 외부 조인(outer join), 세미 조인(semijoin) 등
(4.1, 4.2) 편의유도 연산자 – 조인 연산자 - 세타 조인 (theta join)과 동등 조인 (equijoin)
- 두 릴레이션 R(A1, A2, ..., An)과 S(B1, B2, ..., Bm)의 세타 조인의 결과는 차수가 n+m이고,
애트리뷰트가 (A1, A2, ..., An, B1, B2, ..., Bm)이며,
조인 조건을 만족하는 투플들로 이루어진 릴레이션
- 세타는 {=, <>, <=, <, >=, >} 중의 하나
- 동등 조인은 세타 조인 중에서 비교 연산자가 =인 조인
(4.3) 편의유도 연산자 – 조인 연산자 – 자연 조인 (natural join)
* 표기법 : r ⋈ s
- 동등 조인의 결과 릴레이션에서 조인 애트리뷰트를 제외한 조인
- 여러 가지 조인 연산자들 중에서 가장 자주 사용됨
- 실제로 관계 데이터베이스에서 대부분의 질의는 실렉션, 프로젝션, 자연 조인으로 표현 가능
(5) 디비전 연산자, 나누기 계산 (Division Operation)
* 표기 : r ÷ s
- 차수가 n+m인 릴레이션 R(A1, A2, ..., An, B1, B2, ..., Bm)과 차수가 m인 릴레이션 S(B1, B2, ..., Bm)의
디비전 R ÷ S는 차수가 n이고,
S에 속하는 모든 투플 u에 대하여 투플 tu (투플 t와 투플 u을 결합한 것)가 R에 존재하는 투플 t들의 집합.
(6) 편의유도 연산자 – 배정연산 (Assignment Operation)
- 배정 연산(<-)은 복잡한 질의를 편리하게 표현하는 방법을 제공한다.
- 질의를 일련의 배정 연산과 질의의 결과 값이 디스플레이되는 표현식으로 구성된 순차 프로그램으로 작성한다.
3.4) 추가된 관계 대수 연산자
(1) 외부 조인 (Outer Join)
* 정보의 손실을 피하는 죠인 연산의 확장
- 죠인을 계산하고 다른 릴레이션의 튜플과 부합하지 않는 어떤 릴레이션의 튜플들을 죠인의 결과에 추가한다.
- 왼쪽 외부 조인(left outer join), 오른쪽 외부 조인(right outer join), 완전 외부 조인(full outer join)
(2) 그룹화
(3) 확장 관계형 대수 연산 – 일반화 추출
(4) 확장 관계형 대수 연산 – 집단 함수 (Aggregate Functions)
'프로그래밍 공부 > DataBase (DB)' 카테고리의 다른 글
| [ 데이터베이스 이론 ] 공부 정리 - 4강. SQL INSERT, DELETE, UPDATE문 (0) | 2023.05.19 |
|---|---|
| [ 데이터베이스 이론 ] 공부 정리 - 4강. SQL SELECT문 (1) | 2023.05.19 |
| [ 데이터베이스 이론 ] 공부 정리 - 2강. 관계 데이터 모델과 제약조건 (0) | 2023.05.17 |
| [ 데이터베이스 이론 ] 공부 정리 - 1강. 데이터베이스 시스템 (1) | 2023.05.17 |
| [ 데이터베이스 이론 ] 공부 정리 - 목차 (0) | 2023.05.16 |